▶¿Qué son las RAZONES TRIGONOMÉTRICAS? con ejemplos y ejercicios

La trigonometría es la rama de la matemática que estudia las relaciones numéricas entre los lados y los ángulos de los triángulos.

Al realizar la división entre la medida de lados de un triángulo, sin modificar el ángulo, el resultado independientemente de la longitud de los lados, será siempre el mismo.

Veamos cuantas razones podemos obtener con los lados de un triángulo:

A cada una de estas relaciones se les conoce como seno, coseno, tangente, cosecante, secante y cotangente

Razón trigonométrica en un triángulo rectángulo: valor que se obtiene al comparar dos lados de dicho triángulo con respecto a uno de sus ángulos agudos.

Si consideramos los catetos respecto al ángulo $a$ , a es el cateto opuesto (co), b es el cateto adyacente (ca) y c la hipotenusa (h). Así las razones trigonométricas son:

Ahora veamos cual es el valor de las razones trigonométricas cuando el ángulo no forma un triángulo rectángulo

1.- Consideremos un ángulo $a$ que se encuentra ubicado en el tercer cuadrante

2.- Ahora se toma un punto p(x,y) cualquiera en el lado terminal del ángulo

3.- Se determina r, la distancia desde P hasta el origen O, para ello se aplicará el teorema de Pitágoras

4.- Para determinar las razones trigonométricas se aplicarán las definiciones:

Ejemplos:

a) Determine las razones trigonométricas de un ángulo ubicado en el tercer cuadrante. Considere el punto P(-5,-4)

Aplicamos Pitágoras para determinar r:

Así tenemos que sustituyendo en las definiciones de las razones trigonométricas resulta:

b) Determine las razones trigonométricas de un ángulo ubicado en el cuarto cuadrante. Considere el punto P(3,-4)

Aplicamos Pitágoras para determinar r:

Así tenemos que sustituyendo en las definiciones de las razones trigonométricas resulta:

c) Dado el triángulo rectángulo, determine las razones trigonométricas para el ángulo $\theta$ .

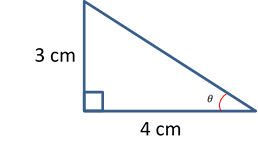
Debemos conocer la longitud de los tres lados del triángulo, por lo que en este caso procederemos a calcular la longitud de la hipotenusa:

1.- Determinemos el valor de los catetos respecto al ángulo $\theta$

2.- Aplicamos el teorema de Pitagóras

Así las razones trigonométricas son:

Ejercicios:

1.- Determine las razones trigonométricas inversas de los ejemplos a), b), c)

2.- Determine las razones trigonométricas de un ángulo ubicado en el primer cuadrante.

3.- Determine las razones trigonométricas de un ángulo ubicado en el segundo cuadrante.

4.- Determine las razones trigonométricas dado un triángulo rectángulo.