Es el proceso inverso al producto notable. Consiste en obtener los factores del polinomio. Por lo que factorizar una expresión algebraica consiste en escribirla como un producto.
En general, cuando se tiene un polinomio y deseamos obtener el producto notable, bastará con factorizar el polinomio, descomponiendo en tantos factores como sea posible.
Como la factorización es la operación matemática que permite descomponer una expresión algebraica en dos más factores, al tener un polinomio que queremos factorizar, en muchos de los casos, se debe escribir como su producto notable.
Por ejemplo:
Existen varios casos de factorización:
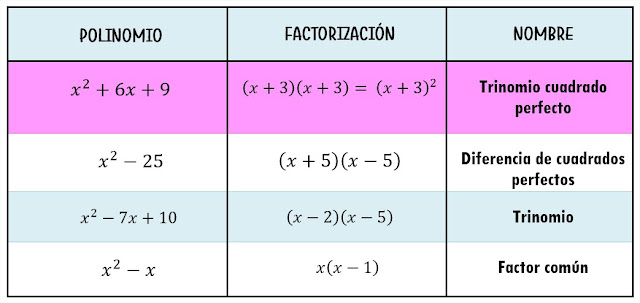
Trinomio cuadrado perfecto
.jpg)
Por ejemplo:
a) $x^{2}+6x+9=(x+3)^{2}$
b) $16x^{2}-40xy+25y^{2}=(4x-5y)^{2}$
c) $4A^{2}B^{2}+20AB+25=(2AB+5)^{2}$
d) $4(m-n)^{2}+12(m-n)+9=(2(m-n)+3)^{2}$
Diferencia de cuadrados perfectos
Los números o las expresiones algebraicas al
elevarlas al cuadrado se obtienen cuadrados perfectos.
_2.jpg)
Por ejemplo:
Factorizar el polinomio
a) $x^{2}-25=(x+5)(x-5)$
b) $16m^{2}-81=(4m+9)(4m-9)$
c) $4a^{6}b^{8}-36=(2a^{3}b^{4}+6)(2a^{3}b^{4}-6)$
d) $(x-1)^{2}-(y+2)^{2}=[(x-1)+(y+2)][(x-1)-(y+2)]$
$=[x+y+1][x-y-3]$Trinomio de la forma $x^{2}+bx+c$
Por ejemplo:
Factorizar el polinomio
Para encontrar el
otro término buscaremos dos números que multiplicados den 10 y sumados sea -7
Las posibles
parejas serán
Observe que la pareja de números que cumple
con las condiciones son el -2 y el -5
Resultando que la manera factorizada del binomio será:
$$x^{2}-7x+10=(x-2)(x-5)$$
b) $x^{2}+8x+15=x^{2}+(5+3)x+5.3=(x+5)(x+3)$
c) $y^{2}-5y-24=y^{2}+(-8+3)y-8.3=(y-8)(y+3)$
d) $m^{2}+3m-18=m^{2}+(6+(-3))m+6*(-3)=(m+6)(m-3)$
Factor común
Un factor común, en un polinomio, es un elemento que está
contenido en todos y cada uno de los términos del polinomio.
La factorización por factor común es el proceso inverso a la aplicación de la propiedad
distributiva. En este caso, las expresiones no tienen un número específico de
términos.
Regla práctica para factorizar un polinomio como factor común monomio
- Factor común:
- Se halla el M.C.D de los coeficientes (si los hay).
- Se toma de la parte literal el factor común que tenga el menor exponente.
- Se multiplica los dos resultados. Este será el factor común.
- Se divide cada uno de los términos de la expresión original entre el factor común, colocando su resultado dentro de paréntesis y multiplicando el factor común.
Por ejemplo:
Factor común polinomio
Sucede cuando en los términos existe factores que
constan de dos o más términos
Por ejemplo:
Factorizar el polinomio
a) $2(m+n)+x(m+n)$
b) $2x(a+b+c)-y(a+b+c)$
EJERCICIOS
1.- Factorice los trinomios cuadrados perfecto:
2.- Factorice aplicando
la
diferencia de dos
cuadrados:
3.- Factoriza los
siguientes trinomios
en dos binomios:
4.- Halla
el factor común de los siguientes ejercicios:
5.- Halla
el factor común de los siguientes ejercicios.
